本文介绍泊松分布和泊松函数的定义,并通过 Python random 库对泊松分布进行仿真,带你触摸复杂表象下的简单本质。
GitHub 项目地址:python-tips/poisson
1. 从泊松函数讲起
泊松分布 表示在给定时间段内发生给定数量的事件的概率。这个定义比较抽象。举个具体的例子,假设你每小时接到电话的概率是固定的,比如每小时 0.05 个,那么你在接下来 1 小时内接到电话个数的概率,就服从泊松分布:
1 小时内接到 0 个电话,对应一个概率值 $P_0$;
1 小时内接到 1 个电话,对应一个概率值 $P_1$;
… …
1 小时内接到 n 个电话,也对应一个概率值$P_n$。
这些概率值组成一个概率分布列,它们的值 $(n, P_n)$ 在二维坐标下连成一条曲线。这条曲线所在的函数就是泊松分布的概率密度函数。其公式及图像如下:
$$\boxed{P(k | t, \lambda)=\frac{(\lambda t)^{k}}{k !} \exp (-\lambda t)}$$
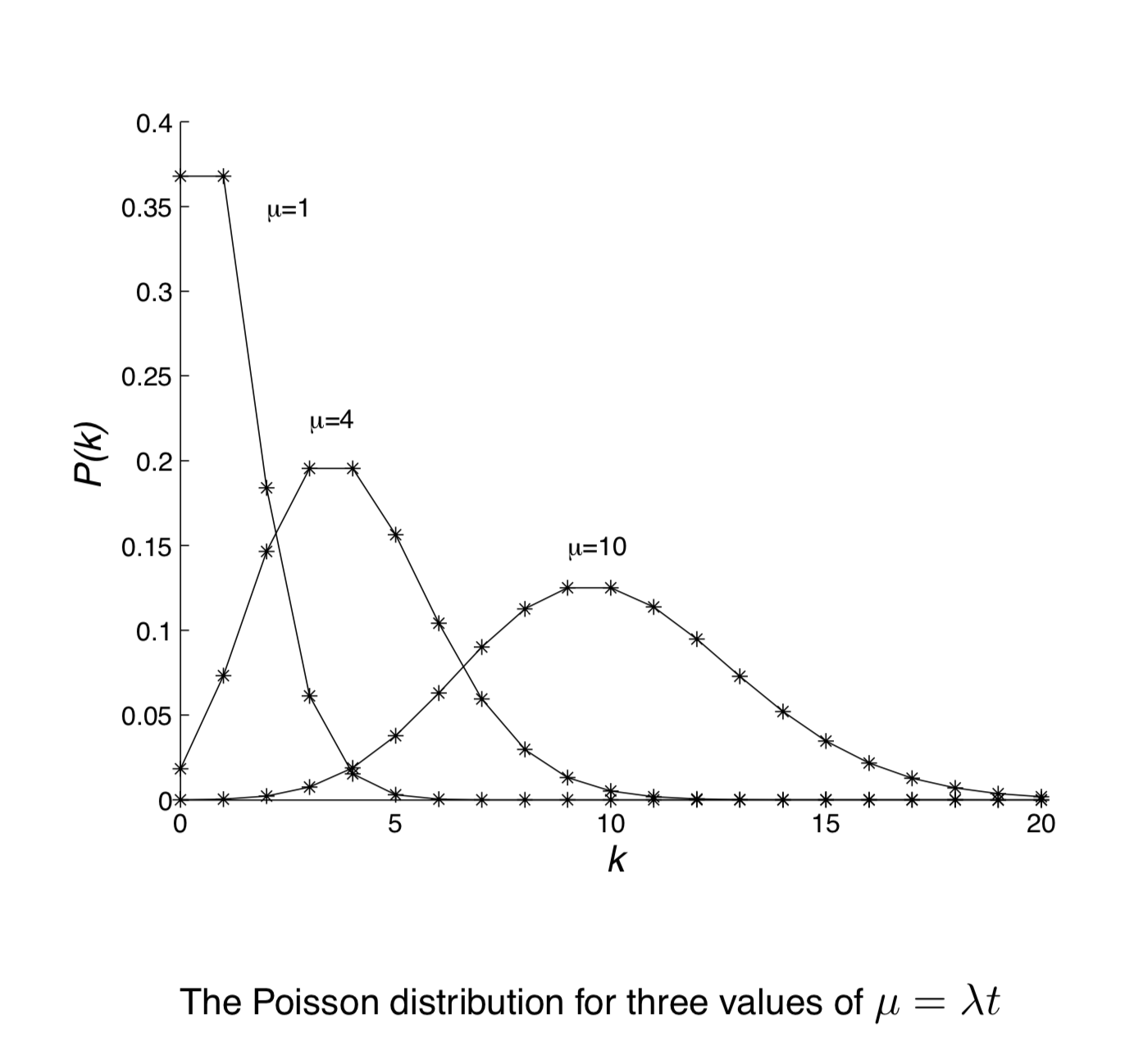
从公式中,我们可以看出:只要确定了 $\lambda$ 和 $t$,该式就退化成了概率 $P$ 关于事件发生次数 $k$ 的函数。 类似地,如果我们确定了 $\lambda$ 和 $k$,则该式退化成概率$P$ 关于时间范围 $t$ 的函数。
“确定哪些参数,让函数最终退化成哪些参数的函数”,这个选择和我们的研究目的有关。如果你对不同 $k$ 如何影响 $P$ 值感兴趣,那么就应该确定参数 $\lambda$ 和 $t$。如果对 $t$ 和 $P$ 之间的关系感兴趣,那么就应该确定参数 $\lambda$ 和 $k$。
$\lambda$, $k$, $t$ 的定义:
$\lambda$: 单位时间内,事件发生的频率$k$: 事件发生次数$t$: 观测事件发生次数的时间范围
$\lambda$, $k$, $t$ 三者的关系:
泊松分布衡量的是多长时间内,某事件发生多少次的概率。这里 $t$ 指代的是多长时间;$k$ 指代的是某事件发生多少次。$\lambda$ 则类似该事件的一个固有属性,$\lambda$ 越大,可以简单理解为该事件在一段时间内发生的概率越大。
Note:
$t$的量纲必须和$\lambda$的量纲相对应。如果$\lambda$的单位是次/小时,则$t$应该取小时为单位;如果$\lambda$的单位是次/分钟,则$t$也应该取分钟为单位。
2. 引入一个实例
接下来我们用一个直观的实例,解释泊松分布在实际问题中是如何运用的。
Q: 一个淘宝客服,平均每 10 分钟接听 1 个电话,那么他连续 1 小时没接到任何电话的概率是多少?
A: $P\left(k=0 | t=1, \lambda=6\right)=\exp \left(-6\right)=0.0024$
其中,$t = 1 小时,\lambda = 6 次/小时$。
我们发现,这个概率是极低的。这说明该客服也许正在上夜班,或者电话断线了,总之他很可能处在一种非正常的状况下。否则在正常情况下,连续 1 小时没接到任何电话的概率仅有千分之二,是极其罕见的。
3. 泊松分布的本质
尽管泊松分布的函数形式看起来很复杂,但它本质上其实很简单。泊松函数的本质,也就是它的基本假设,可以追溯到一个简单的公式:
$$\boxed{P = \lambda \Delta t}$$
这个公式看起来太过简单,以至于你可能不相信它能推导出上文那个复杂的泊松分布函数。如果你想了解推导过程,可以看我之前写的博客 排队论在网络性能分析中的应用,里面有详细证明。本文的主题不在于此,就不展开讲了。
4. 建模仿真
这个简单公式,就是泊松分布的核心假设。也就是说,我们只需要用这个公式,就能对泊松分布做仿真了。
这里还有个技巧。因为在假设中,$\Delta t$ 代表无限小的时间间隔,但在编程中,我们没法写出无限小这种东西(其实可以,求别杠)。因此只能量力而行。比如,如果 $t$ 代表一个小时,而 $\lambda$ 表示 20 次每小时,则我们的时间片只要切到比 20 这个数字大一到两个数量级即可。20 是的数量级是十,大两个数量级是千。这里我们把一小时时间切割为一千个时间片,并将每个时间片内事件发生的概率设为 20⁄1000,就保证了一小时内,事件发生次数的期望是 20 了。也就在千分之一小时的精度内,满足了 $P = \lambda \Delta t$ 这个公式。
OK,闲言少叙,我们这就开始建模仿真。
# -*- coding: utf-8 -*-
"""泊松仿真
author: github@luochang212
usage: python poisson.py [RATE] {TIME}
"""
import sys
import random
import collections
import matplotlib.pyplot as plt
class Poisson:
def __init__(self, rate=sys.argv[1]):
self.rate = int(rate)
self.time = 1 # 单位时间
if len(sys.argv) > 2 and sys.argv[2] != "":
self.time = int(sys.argv[2]) # 手动指定时间范围
self.EXP_NUM = 100000 # 实验次数
self.NUM_LEVEL = 2 # 数量级
def generator(self, prob):
"""仿真结果生成器"""
while True:
if random.random() < prob:
yield 1
else:
yield 0
def perform_exp(self, rate, time):
"""进行一次实验
每次实验中,时间分片的数量比rate高两个数量级
"""
level = len(str(rate))
shard_num = 10 ** (level + self.NUM_LEVEL) # 计算时间分片的数量
gen = self.generator(rate / shard_num)
cnt = 0
for _ in range(time * shard_num):
cnt += next(gen)
return cnt
def perform_exps(self, exp_num, rate, time):
"""多次实验,得到分布"""
lst = []
for _ in range(exp_num):
lst.append(self.perform_exp(rate, time))
return sorted(collections.Counter(lst).items(), key=lambda e: e[0])
def draw(self, sorted_list):
"""画图"""
s = sum([e[1] for e in sorted_list])
x = [e[0] for e in sorted_list]
y = [e[1] / s for e in sorted_list]
plt.plot(x, y)
plt.xlabel("k")
plt.ylabel("P(k)")
plt.show()
def main(self):
sorted_list = self.perform_exps(self.EXP_NUM, self.rate, self.time)
self.draw(sorted_list)
@staticmethod
def calculator(rate, t, k):
"""用于计算泊松函数的概率 P(k|t,lambda)
rate: lambda
t: t
k: k
"""
import math
return (rate * t) ** k / math.factorial(k) * math.exp(-rate * t)
if __name__ == '__main__':
p = Poisson()
p.main()
看完代码,聪明的你一定已经知道这段代码在干什么了
那我们直接来说如何使用代码吧!
如果你想知道 $\lambda = 3, t = 2$ 情况下泊松函数的图像,在命令行执行:
python poisson.py 3 2
如果不设置 $t$ 的值,则 $t$ 的值默认为 1。
下面放一些仿真结果:
$\lambda = 2, t = 1$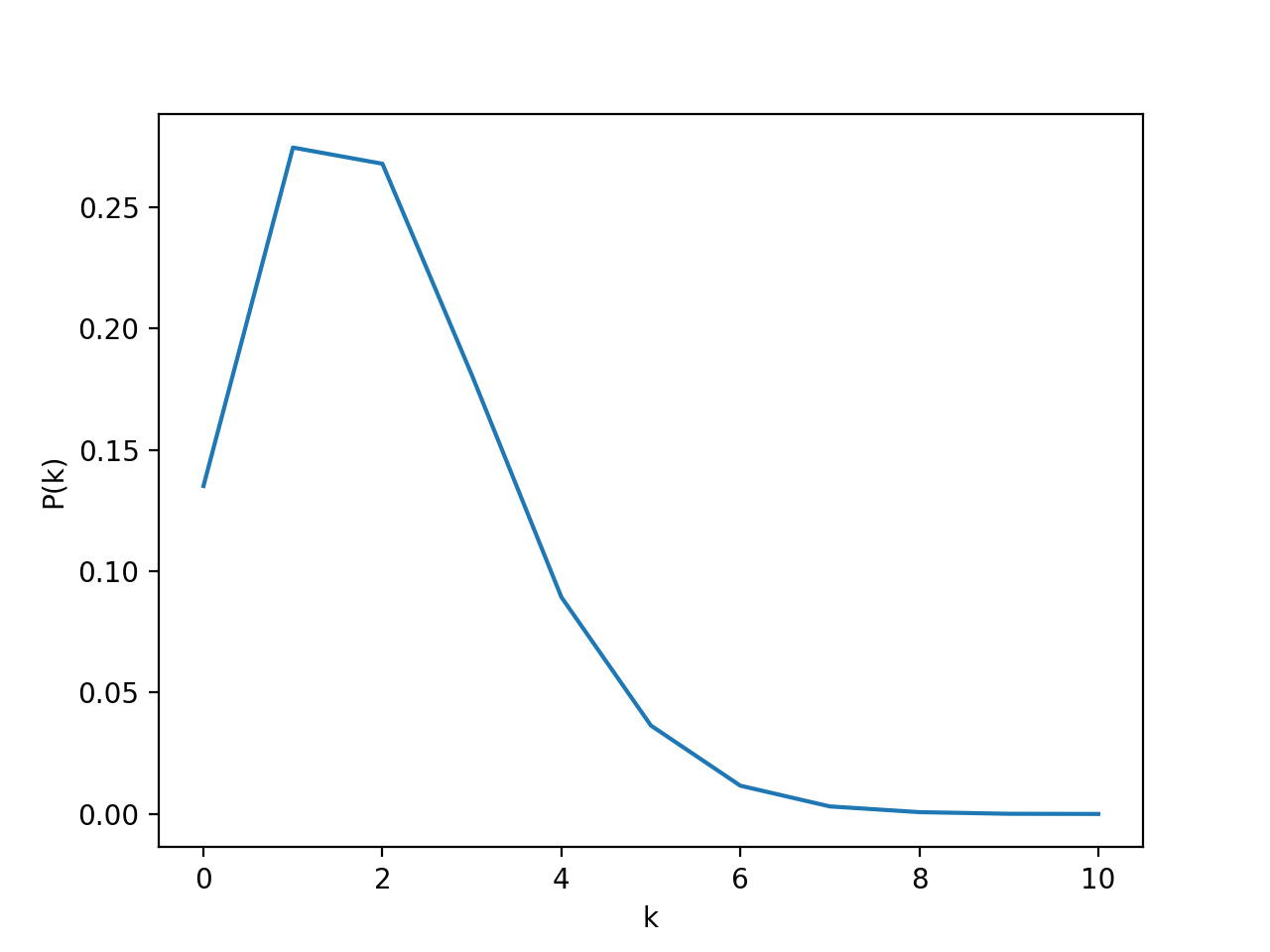
$\lambda = 5, t = 1$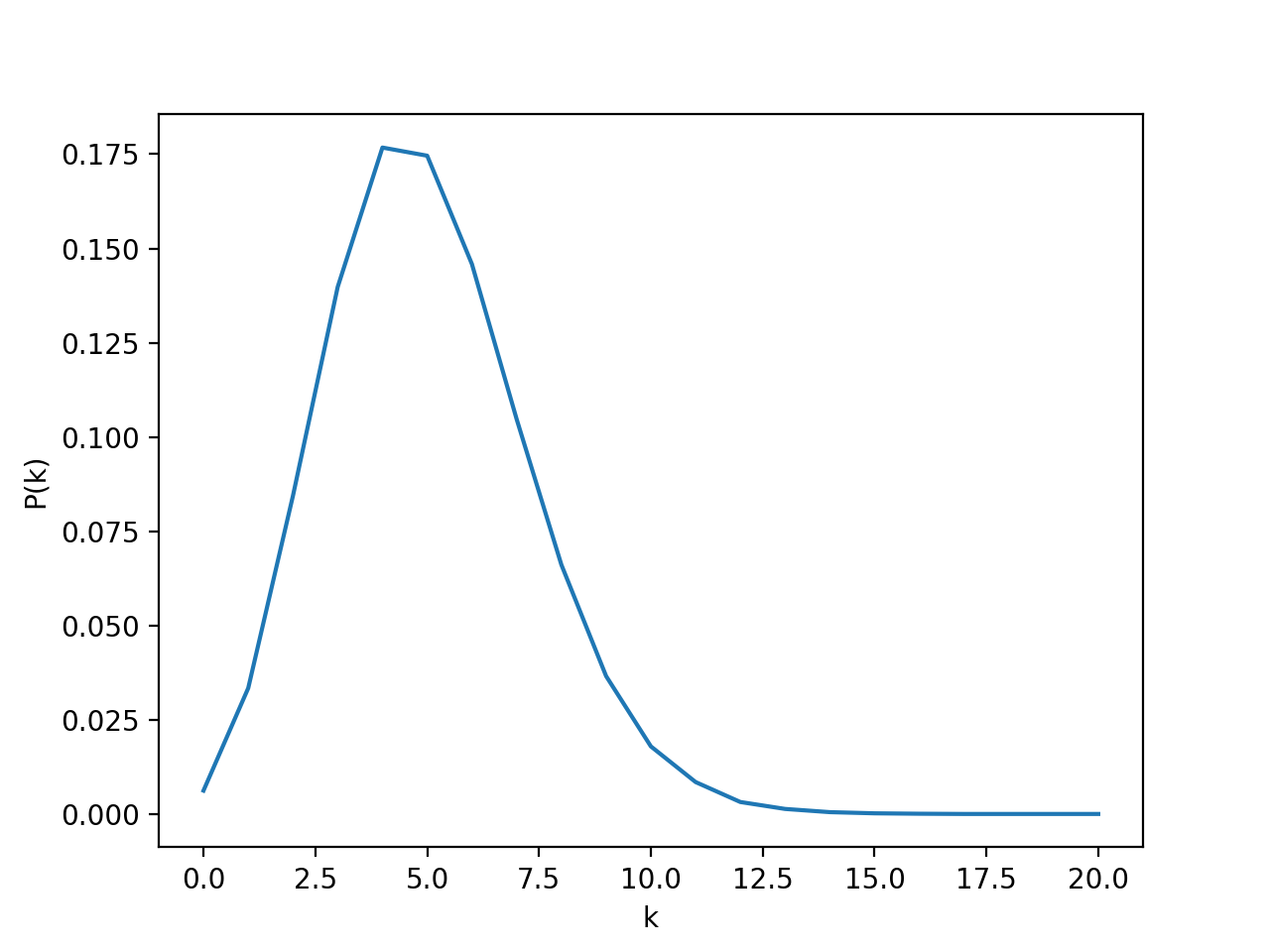
$\lambda = 10, t = 1$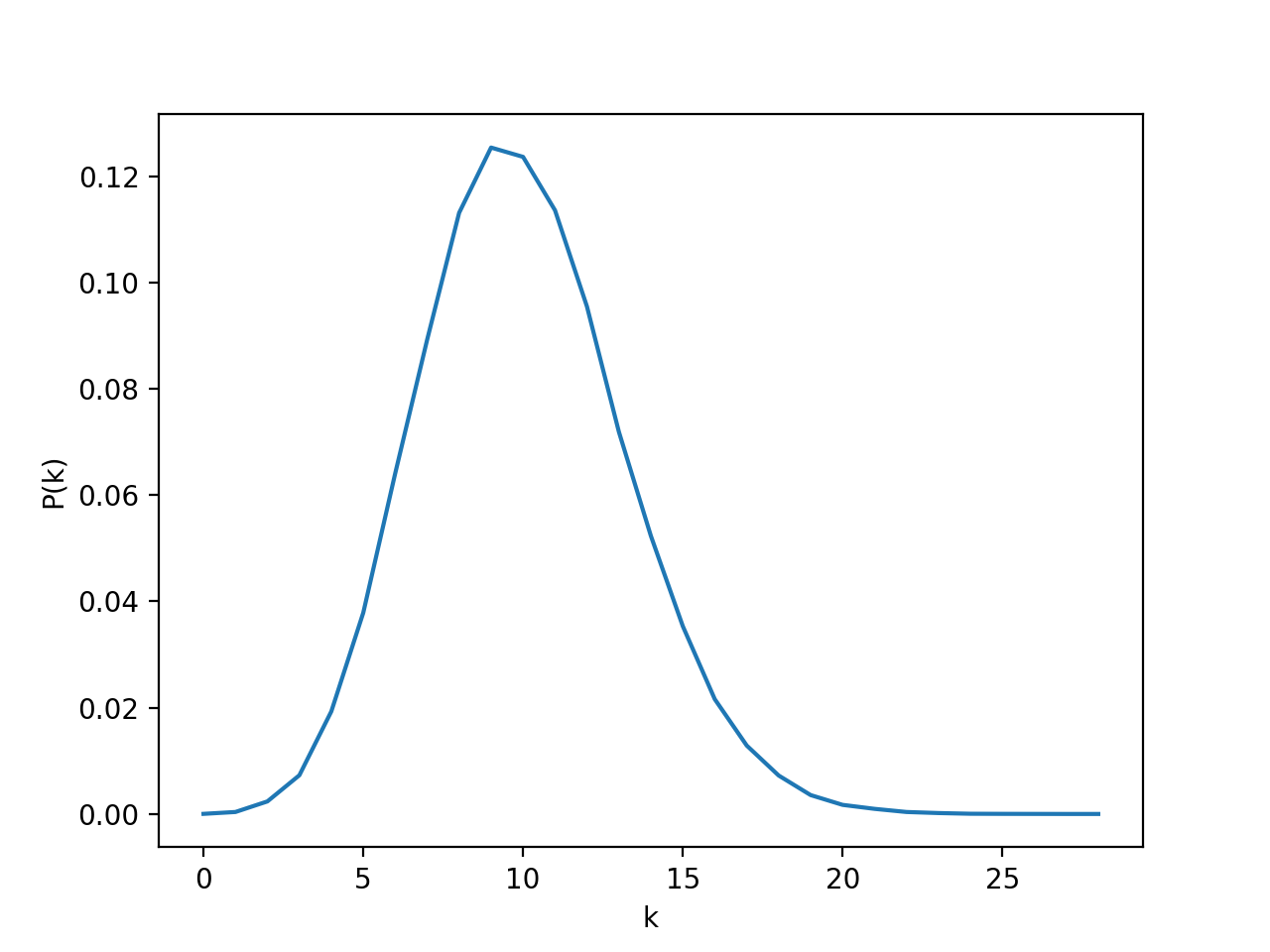
$\lambda = 80, t = 1$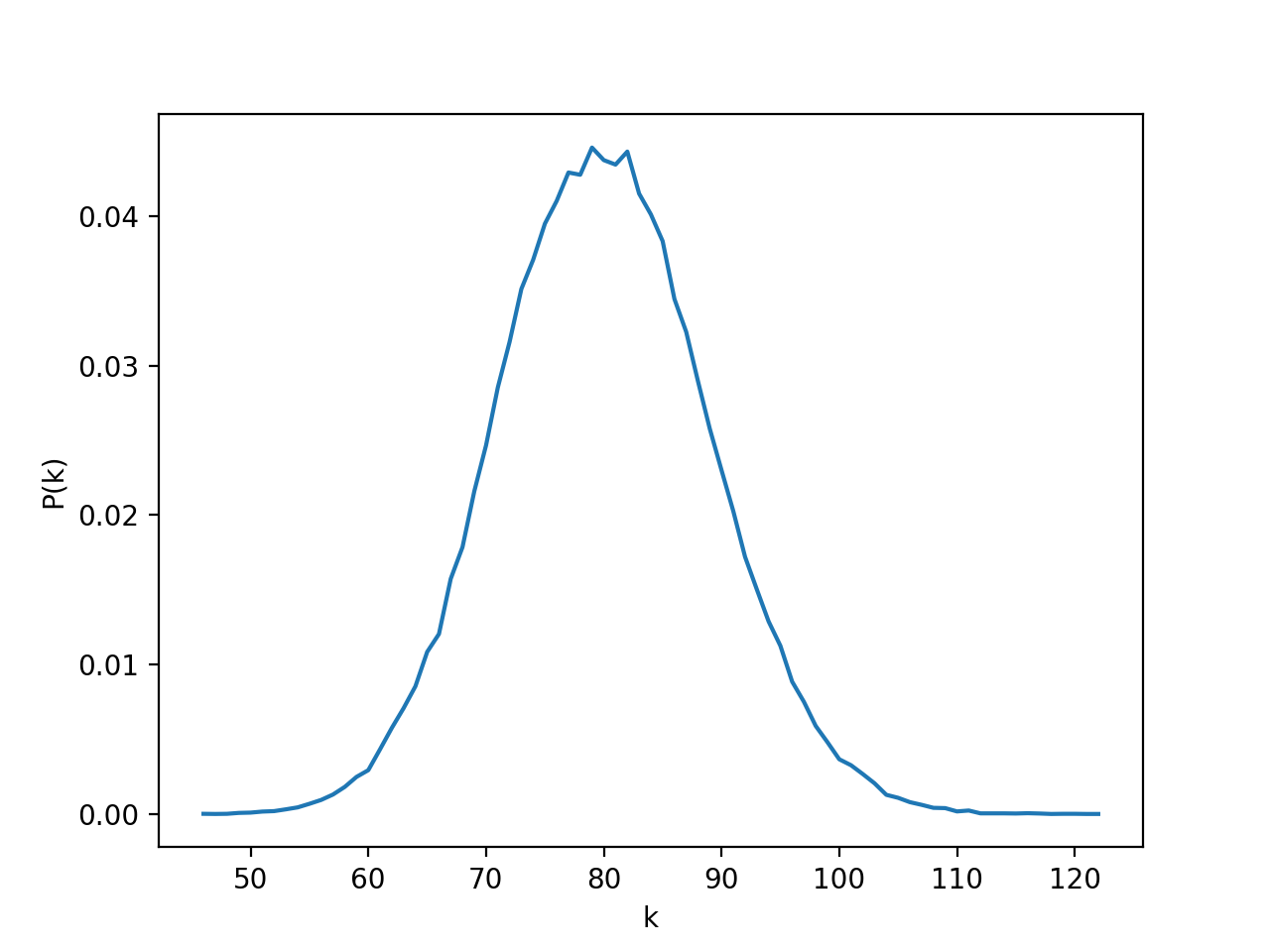
5. 三维可视化
泊松分布有三个自变量,一个因变量,需要四维空间才能把它完整地绘制出来。但幸好,通过观察我们发现 $\lambda$ 和 $t$ 的关系很近,可以归约成一个变量 $\mu$。我们设 $\mu = \lambda t$,则绘制 $P = f(\mu, k)$ 的图像,就足以表达泊松函数四个变量间的函数关系了。
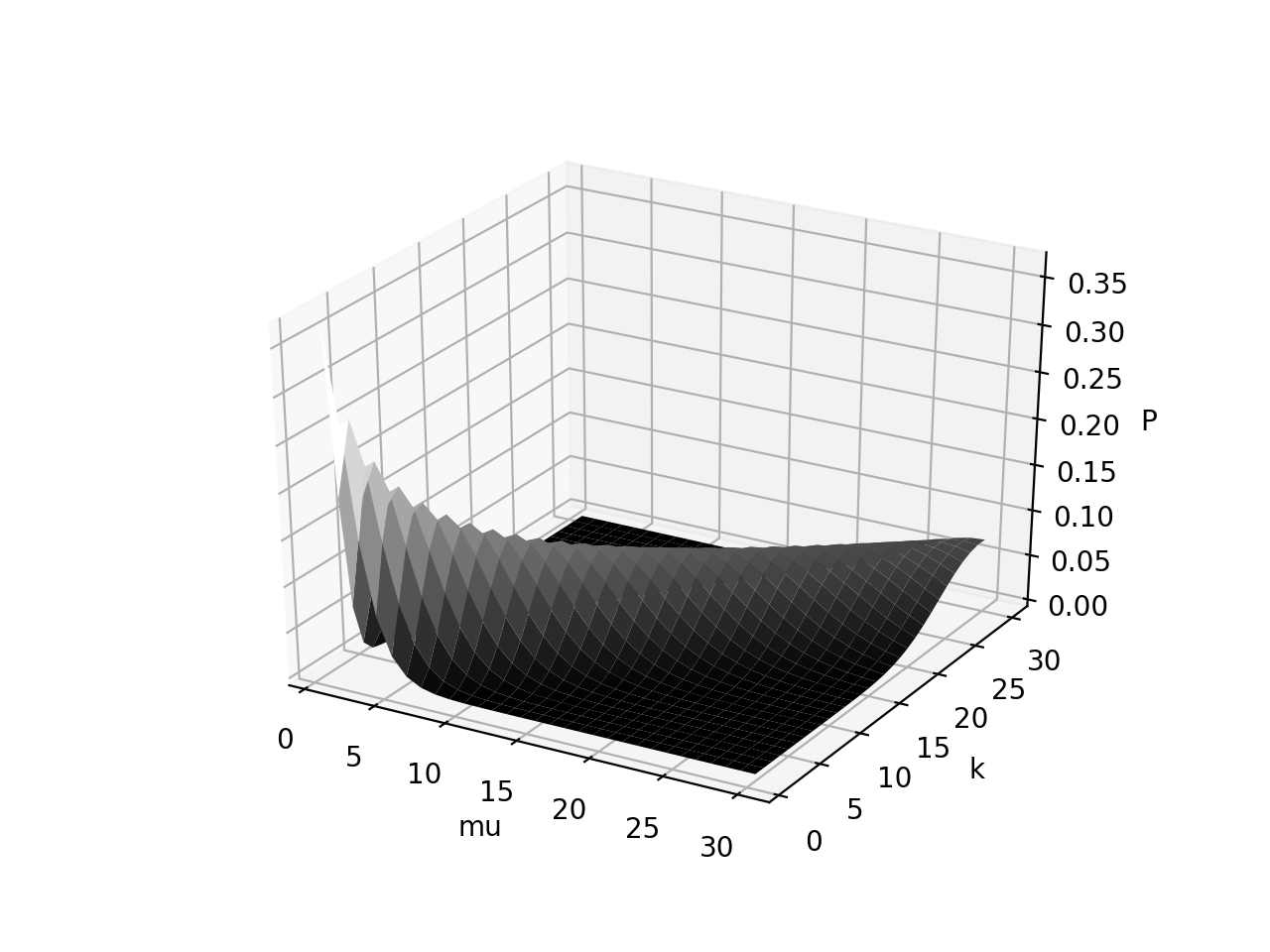
Note: 绘图代码见 3dplot.py

