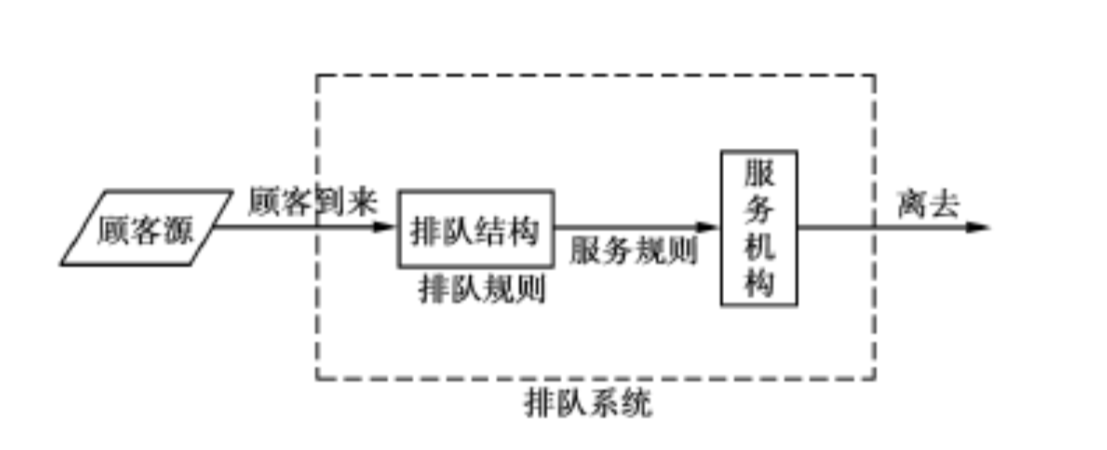
排队论(queueing theory)也称随机服务系统理论,它研究的内容有三部分:性态问题、最优化问题和统计推断问题。(《运筹学》清华大学出版社)
下图描述了排队过程的一般流程:
现实中的排队问题是多种多样的,对上述“顾客源”和“服务机构”应该作宽泛的理解。顾客和服务机构可以是生物,也可以是非生物;排队结构可以是有形的,也可以是无形的,比如向交换台要求通话的请求;顾客可以走向服务机构,也可以相反,比如送货上门。
在网络中,服务器和用户之间相互传送数据包。数据包的传送需要时间,因此或多或少都会产生延迟。为了分析这些延迟,我们引入了一系列假设,并利用排队论对网络延迟进行建模分析。
本文将着重介绍网络性能分析(Network performance analysis)中几种常见的排队模型。它们是:
- The M/M/1 queuing system
- The birth-death process
- The M/M/m queuing system
- The M/M/1/m queuing system
- The M/M/∞ queuing system
- The M/M/m/m queuing system
另外,作为以上模型的理论基础,本文将首先介绍泊松过程(Poisson process)。
泊松过程的推导
泊松过程是马尔可夫过程的一个特例,在排队论中经常被用来估计顾客到达的概率分布。
(一)泊松过程的假设
-
在时间间隔$\Delta t$内,有且仅有一位顾客到达的概率$P$和$\Delta t$成比例,比例系数为$\lambda$
-
在时间间隔$\Delta t$内,至多只允许一位顾客到达(否则应该选取一个更短的时间间隔)
$$\begin{aligned} P(\text { 在时间间隔 }[t, t+\Delta t] \text { 内,有且仅有一位顾客到达 }) &=\lambda \Delta t \\ P(\text { 在时间间隔 }[t, t+\Delta t]\text { 内,没有顾客到达 }) &=1-\lambda \Delta t \\ P(\text { 在时间间隔 }[t, t+\Delta t]\text { 内,多于一位顾客到达 }) &=0 \end{aligned}$$ -
泊松过程是对顾客到达过程的估计,故不考虑顾客的离开情况,所以到达人数只增不减
-
只考虑一阶无穷小对结果的影响,忽略二阶无穷小,$\Delta t \gg(\Delta t)^{2} \approx 0$
-
$P_{k}(t)$表示在时间间隔$t$内有k位顾客到达的概率
-
$p_{i, j}(\Delta t)$表示在时间间隔$\Delta t$内到达总人数由$i$变为$j$的概率
(二)推导过程
泊松过程的状态转移图如下:
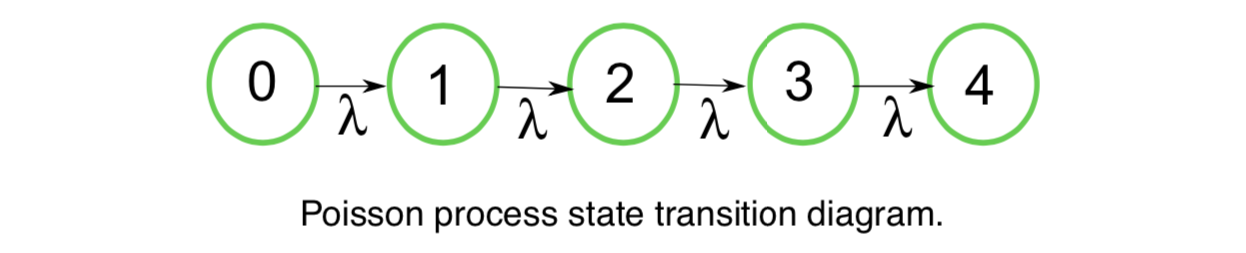
由于总人数单调递增,且在时间间隔$\Delta t$内,到达总人数最多增加1。因此,如果$t+\Delta t$时刻的到达人数是k,那么在$t$时刻的到达人数只有两种情况:k或者k-1.
根据上述推断,时间间隔$t+\Delta t$内到达总人数为k的概率可由时间间隔$t$内到达总人数为k和k-1的概率表示:
$$\begin{aligned} P_{k}(t+\Delta t) &=P_{k}(t) p_{k, k}(\Delta t)+P_{k-1}(t) p_{k-1, k}(\Delta t) \\ P_{0}(t+\Delta t) &=P_{0}(t) p_{0,0}(\Delta t) \quad k=0 \text { (起始状态) } \end{aligned}$$
由泊松过程的假设可知:
$$p_{k, k}(\Delta t)=(1-\lambda \Delta t) \quad \text { and } \quad p_{k-1, k}(\Delta t)=\lambda \Delta t$$
代入上式可得:
$$\begin{aligned} P_{k}(t+\Delta t) &=P_{k}(t)(1-\lambda \Delta t)+P_{k-1}(t)(\lambda \Delta t) \\ P_{0}(t+\Delta t) &=P_{0}(t)(1-\lambda \Delta t) \quad k=0 \text { (starting condition) } \end{aligned}$$
整理得:
$$\begin{aligned} \frac{P_{k}(t+\Delta t)-P_{k}(t)}{\Delta t} &=-\lambda P_{k}(t)+\lambda P_{k-1}(t) \\ \frac{P_{0}(t+\Delta t)-P_{0}(t)}{\Delta t} &=-\lambda P_{0}(t) \end{aligned}$$
当$\Delta t \rightarrow 0$时有:
$$\begin{aligned} \frac{d P_{k}(t)}{d t} &=-\lambda P_{k}(t)+\lambda P_{k-1}(t) \quad (k \geq 1) \quad (1) \\ \frac{d P_{0}(t)}{d t} &=-\lambda P_{0}(t) \quad \quad \quad \quad \quad \quad \quad \quad (2) \end{aligned} $$
解方程(2)可得:
$$P_{0}(t)=A \exp (-\lambda t)$$
其中$A$是任意常数。设方程(1)的$k=1$,把方程(2)的解代入方程(1)中有:
$$\frac{d P_{1}(t)}{d t}=-\lambda P_{1}(t)+A \lambda \exp (-\lambda t)$$
解得:
$$P_{1}(t)=A \lambda t \exp (-\lambda t)$$
$k=2$时同理:
$$\frac{d P_{2}(t)}{d t}=-\lambda P_{2}(t)+A \lambda^{2} t \exp (-\lambda t)$$
解得:
$$P_{2}(t)=\frac{A(\lambda t)^{2}}{2} \exp (-\lambda t)$$
对任意常数k,解为:
$$P_{k}(t)=\frac{A(\lambda t)^{k}}{k !} \exp (-\lambda t)$$
下面计算$A$的值,由于系统处于各状态的概率之和为1,故有:
$$P_{0}(t)+P_{1}(t)+P_{2}(t)+\cdots=\sum_{i=0}^{\infty} P_{i}(t)=1$$
即:
$$A \exp (-\lambda t) \sum_{k=0}^{\infty} \frac{(\lambda t)^{k}}{k !}=1$$
由泰勒展开解得$A=1$。因此,泊松过程的概率密度函数为:
$$\boxed{P(k | t, \lambda)=\frac{(\lambda t)^{k}}{k !} \exp (-\lambda t)}$$
下图是几个不同$\mu$值对应的泊松过程函数图像:
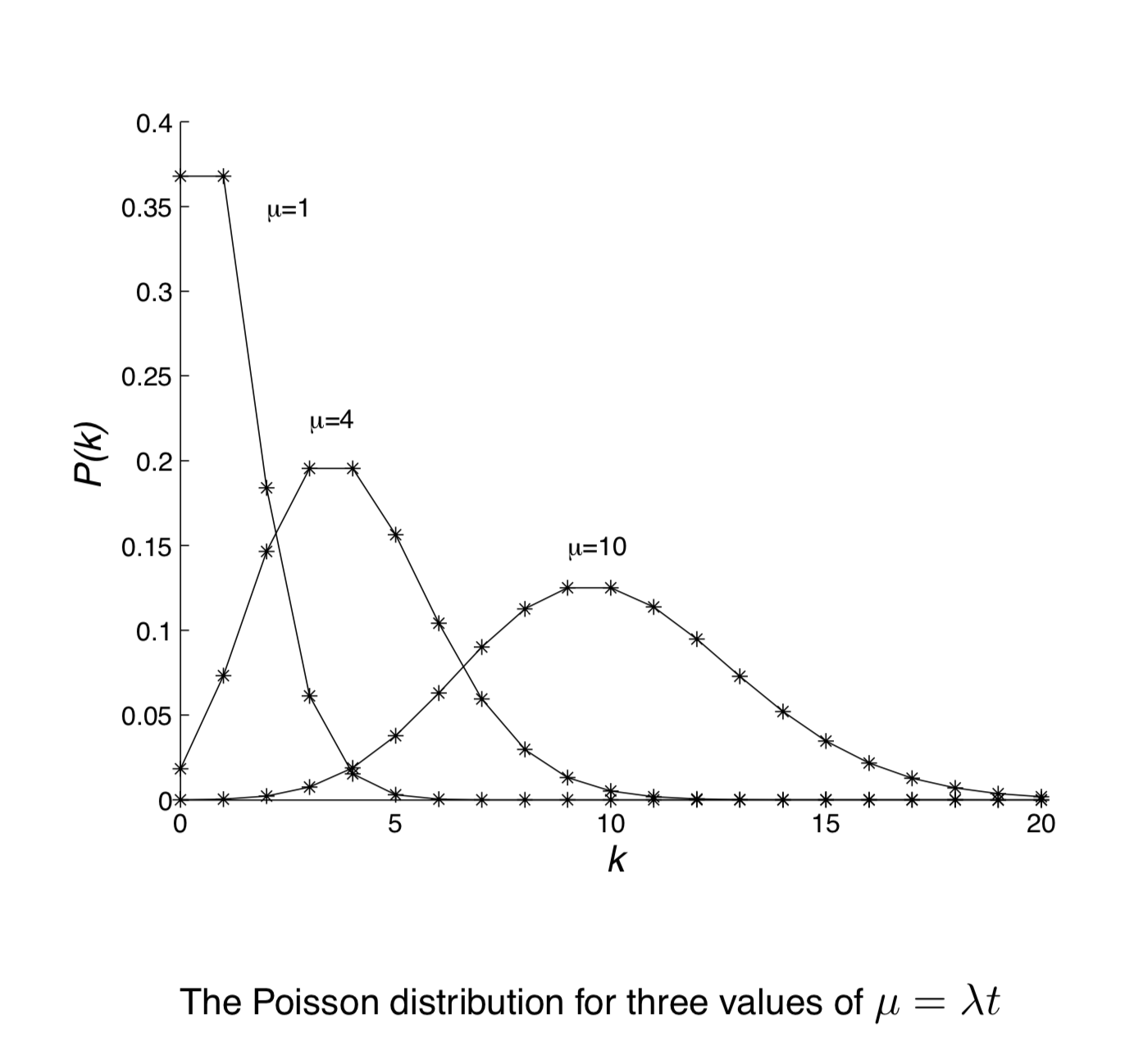
(三)泊松过程实例
一个交换机平均每分钟接收100个电话请求,按照泊松过程,该交换机连续五秒未收到电话请求的概率的多少?
$$P\left(k=0 | t=\frac{1}{12}, \lambda=100\right)=\exp \left(-\frac{100}{12}\right)=0.00024$$
Note: 从上面这个实例我们能看出:k代表顾客的数量,t代表这段时间间隔的长度,$\lambda$代表平均每单位时间到达的顾客数。
排队系统的分类
排队系统的分类用Kendall符号表示,符号形式为:
$$X/Y/Z/A/B/C$$
填写规则如下:
- X 处填写表示相继到达间隔时间的分布;
- Y 处填写表示服务时间的分布;
- Z 处填写并列的服务器的数目;
- A 处填写系统容量限制 N;
- B 处填写顾客源数目 m;
- C处填写服务规则,如先到先服务( FCFS),后到后服务( LCFS)等。
比如,M/M/1 表示相继到达间隔时间为负指数分布、服务时间为负指数分布、单服务器的模型;D/M/5 表示确定的到达间隔、服务时间为负指数分布、5个平行服务器的模型。
Note: 从上述两个例子我们能看出:M代表负指数分布,D代表确定型。这里,M和D是概率分布类型的代号。常见概率分布类型的代号如下:
$M$ —— 负指数分布(M是Markov的字头,因为负指数分布具有无记忆性,即Markov性) ;
$D$ —— 确定型(deterministic);
$E_k$ —— k 阶爱尔朗(erlang)分布;
$GI$ —— 一般相互独立(general independent)的时间间隔的分布;
$G$ —— 一般(general)服务时间的分布。
The M/M/1 queuing system
(一)M/M/1排队系统的假设
M/M/1排队系统是相继到达时间间隔为负指数分布、服务时间为负指数分布、单服务器的模型,且只有一个队列。
M/M/1排队系统的状态转移图如下:
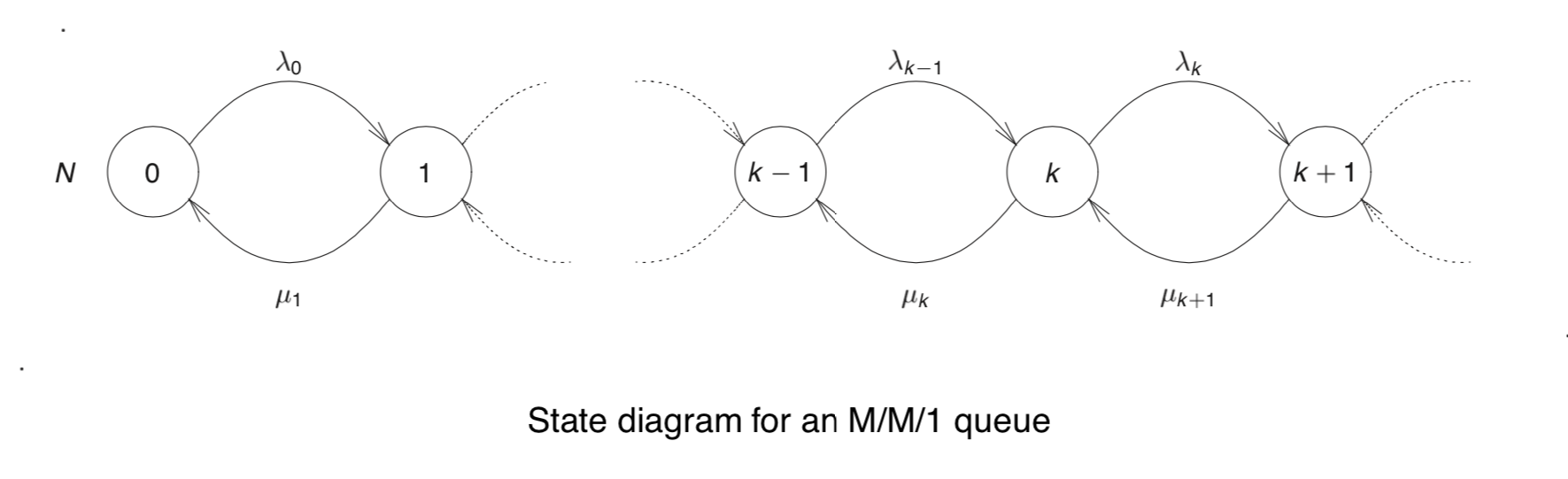
图中,$\lambda_k$表示当系统处于状态k时的到达速率(arrival rate),$\mu_{k}$表示当系统处于状态k时的服务速率(service rate).
Note: M/M/1排队系统的性质:
- 系统处于状态n是指系统内有n位顾客,这n位顾客既包括正在排队的,也包括正在接受服务的;
- 如果状态n的情况已知,那么其他所有关于该队列的信息都可以被推断出来。
(二)推导过程
回忆前文泊松过程的假设:
$$\begin{aligned} P(\text { 在时间间隔 }[t, t+\Delta t] \text { 内,有且仅有一位顾客到达 }) &=\lambda \Delta t \\ P(\text { 在时间间隔 }[t, t+\Delta t]\text { 内,没有顾客到达 }) &=1-\lambda \Delta t \\ P(\text { 在时间间隔 }[t, t+\Delta t]\text { 内,多于一位顾客到达 }) &=0 \end{aligned}$$
上述公式是对到达速率$\lambda$而言的,对服务速率$\mu$也采用相同的模型假设:
$$\begin{aligned} P(\text { 在时间间隔 }[t, t+\Delta t] \text { 内,有且仅有一位顾客服务完成 }) &=\mu \Delta t \\ P(\text { 在时间间隔 }[t, t+\Delta t]\text { 内,没有顾客服务完成 }) &=1-\mu \Delta t \\ P(\text { 在时间间隔 }[t, t+\Delta t]\text { 内,多于一位顾客服务完成 }) &=0 \end{aligned}$$
约定:
- $P_{k}(t)$表示在时间间隔$t$内,系统内有$k$位顾客的概率
- $p_{i, j}(\Delta t)$表示在时间间隔$\Delta t$内,系统内人数由$i$变为$j$的概率
时间间隔$t+\Delta t$内系统内人数为k的概率可由时间间隔$t$内系统内人数为k和k-1的概率表示:
$$\begin{aligned} P_{k}(t+\Delta t)=& P_{k}(t) p_{k, k}(\Delta t)+P_{k-1}(t) p_{k-1, k}(\Delta t) \\ &+P_{k+1}(t) p_{k+1, k}(\Delta t) \\ P_{0}(t+\Delta t)=& P_{0}(t) p_{0,0}(\Delta t)+P_{1}(t) p_{1,0}(\Delta t) \quad k=0 \text { (起始状态) } \end{aligned}$$
和泊松过程比较,M/M/1 排队模型的转移概率多了从状态 k+1 转到状态 k 的一项。点击这里回顾泊松过程的相关公式。
将泊松过程的模型假设公式和M/M/1 排队系统的假设公式,代入上述公式:
$$\begin{aligned} P_{k}(t+\Delta t)=& P_{k}(t)(1-\lambda \Delta t)(1-\mu \Delta t)+P_{k-1}(t)(\lambda \Delta t)(1-\mu \Delta t) \\ &+P_{k+1}(t)(\mu \Delta t)(1-\lambda \Delta t) \\ P_{0}(t+\Delta t)=& P_{0}(t)(1-\lambda \Delta t)+P_{1}(t)(\mu \Delta t)(1-\lambda \Delta t), \quad k=0 \end{aligned}$$
当$\Delta t \rightarrow 0$时有:
$$\begin{aligned} \frac{d P_{k}(t)}{d t} &=-(\lambda+\mu) P_{k}(t)+\lambda P_{k-1}(t)+\mu P_{k+1}(t), \quad k \geq 1 \\ \frac{d P_{0}(t)}{d t} &=-\lambda P_{0}(t)+\mu P_{1}(t) \end{aligned}$$
考虑系统处于稳定状态(steady state)的情况,有:
$$\frac{d P_{k}(t)}{d t}=0, \qquad k \geq 0$$
代入上式可得:
$$\begin{aligned} (\lambda+\mu) P_{k}-\lambda P_{k-1}-\mu P_{k+1} = 0, \quad k \geq 1 \\ \lambda P_{0}-\mu P_{1} = 0, \quad k = 0 \end{aligned}$$
解得:
$$\lambda P_{k-1}=\mu P_{k}$$
Note: 稳定状态下,系统处于状态k的概率是稳定的、不随时间变化的,因此状态k的概率变化率为0,即
$\frac{d P_{k}(t)}{d t}=0$。
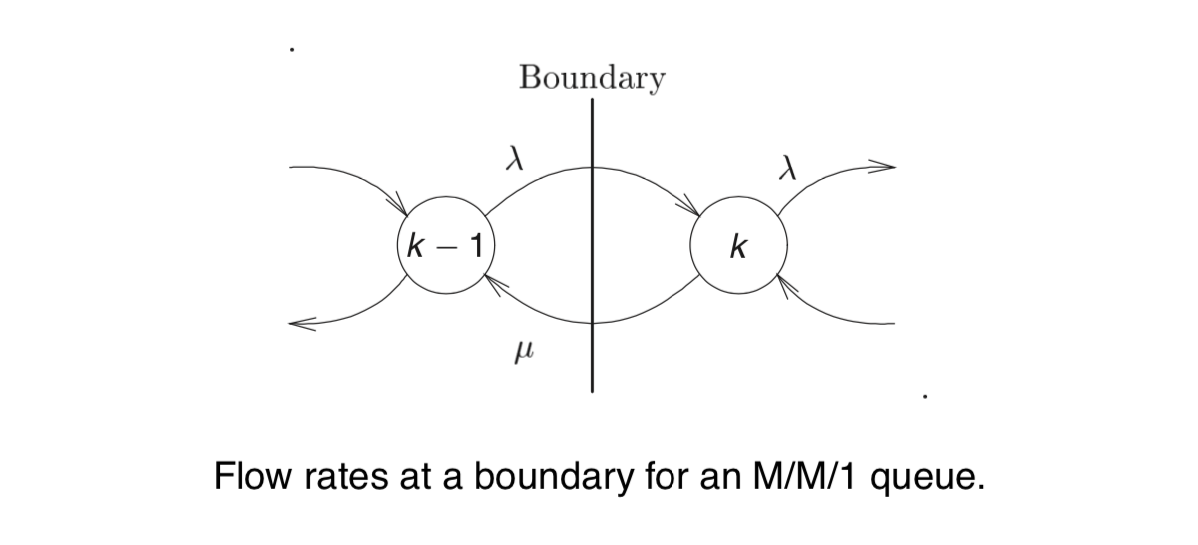
下面是M/M/1 排队系统的通量图,由系统处于各状态的概率不随时间变化可知,从状态k-1转移到状态k的通量和从状态k转移到k-1的通量应该相等。从状态k-1到状态k的通量为
$\lambda P_{k-1}$,从状态k到状态k-1的通量为$\mu P_{k}$。故即使不通过公式推导,我们也能得出$\lambda P_{k-1}=\mu P_{k}$的结论。
整理上式得:
$$P_{k}=\frac{\lambda}{\mu} P_{k-1}$$
递推可得:
$$P_{k}=\left(\frac{\lambda}{\mu}\right)^{k} P_{0}=\rho^{k} P_{0}, \text { 其中 } \rho = \frac{\lambda}{\mu}$$
下面计算$P_{0}$的值,由于:
$$\sum_{k=0}^{\infty} P_{k}=1$$
将$P_{k}=\rho^{k} P_{0}$代入上式有:
$$P_{0} \sum_{k=0}^{\infty} \rho^{k}=1$$
整理得:
$$P_{0}=\frac{1}{\sum_{k=0}^{\infty} \rho^{k}}$$
当$\rho<1$时有:
$$\sum_{k=0}^{\infty} \rho^{k}=\frac{1}{1-\rho} \quad \text { for } \rho<1$$
故:
$$P_{0}=(1-\rho)$$
综上,处于稳定状态的M/M/1 排队系统的概率分布为:
$$\boxed{ P_{k}=\rho^{k}(1-\rho), \rho<1}$$
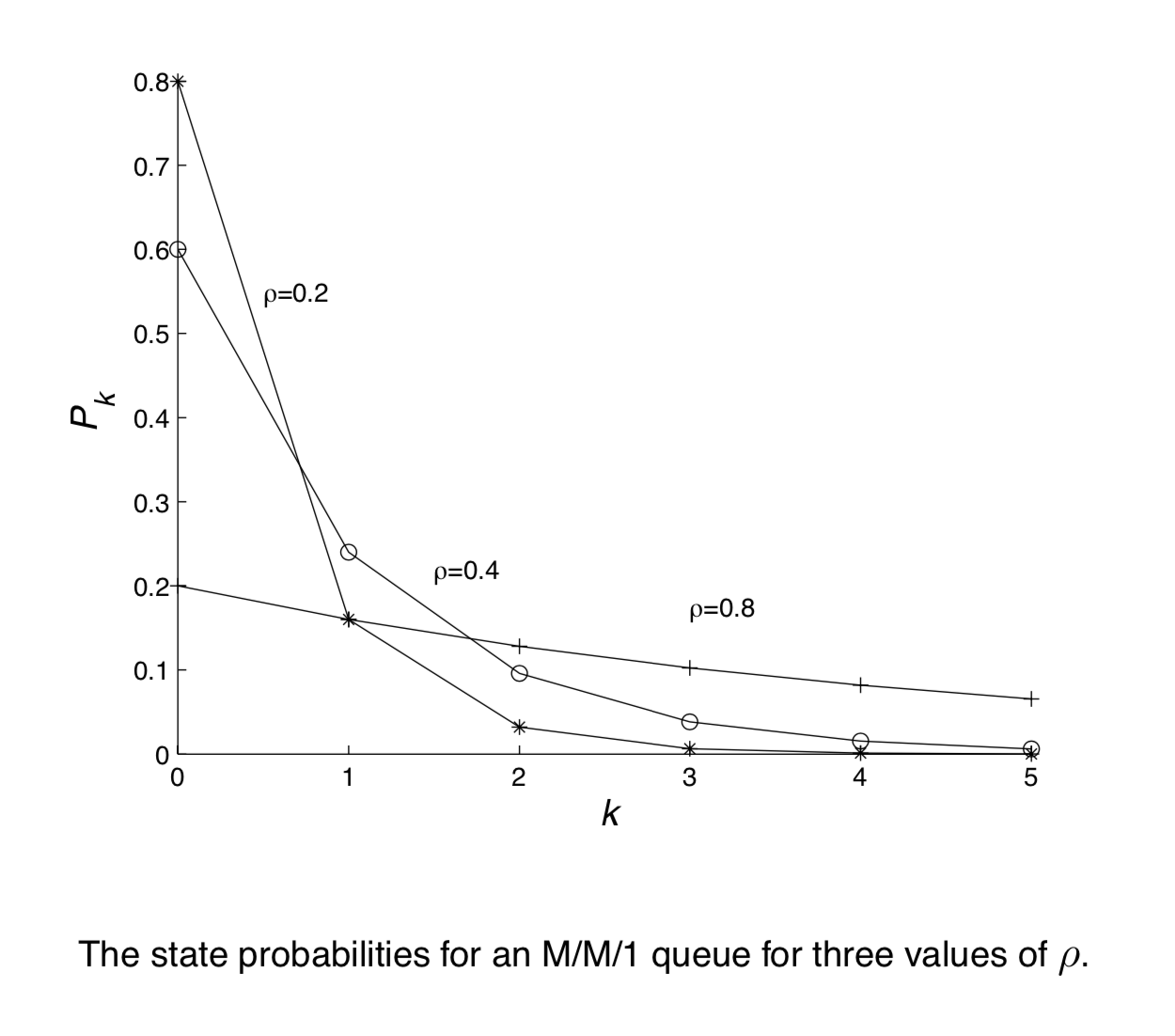
下图是不同的$\rho$值下M/M/1 排队系统概率分布的函数图像:
The birth-death process
Note: The M/M/1 queuing system 和 The birth-death process 之间的关系:
- The M/M/1 queuing system - 只有一个队列,对队列中的顾客数量没有限制;有且仅有一个服务器;稳定状态下,到达速率和服务速率都是常数。
- The birth-death process - 是 The M/M/1 queuing system 的推广。但是,稳定状态时,到达速率和服务速率是相互独立的,到达速率和服务速率随状态k的变化而变化。
从上面的描述我们知道,The M/M/1 queuing system 和 The birth-death process是很相像的,唯一的区别在于系数。在 M/M/1 排队系统中,系数都是常数,而 The birth-death process 中的系数是随状态k的变化而变化的。也就是说,在 The birth-death process 的模型中,只需要把 The M/M/1 queuing system 中所有的$\lambda$和$\mu$替换成$\lambda_k$和$\mu_k$即可。
$\lambda$和$\mu$是所有状态的平均值,而$\lambda_k$和$\mu_k$是状态k下的到达概率通量(arrival probability flux)和服务概率通量(service probability flux)。它们之间的关系可以表示为:
$$\lambda_{k}=\lambda P_{k} \quad \text { and } \quad \mu_{k}=\mu P_{k}$$
The birth-death process 的通量图如下:
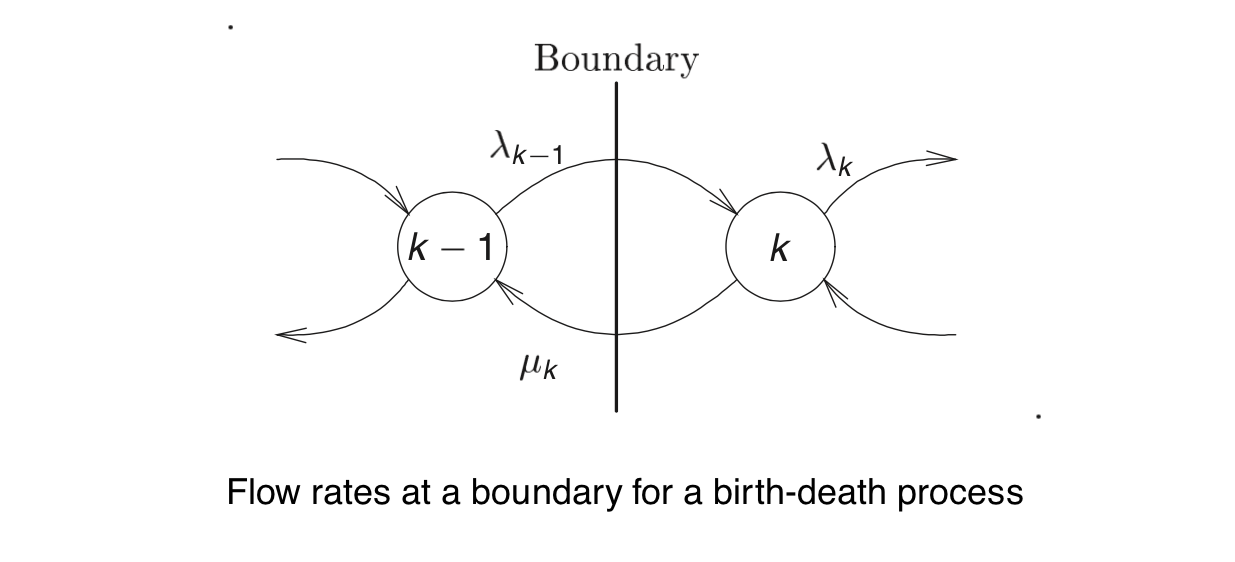
稳定状态下,由经过边界的通量相互抵消可得:
$$\lambda_{k} P_{k}=\mu_{k+1} P_{k+1}$$
后续的推导过程和 M/M/1 排队系统的推导十分相似,就不再赘述了。这里直接给出 The birth-death process 的状态概率分布函数:
$$\boxed{ P_{k}=\left(\frac{\prod_{i=0}^{k-1} \lambda_{i}}{\prod_{i=1}^{k} \mu_{i}}\right) P_{0}, \qquad k \geq 1 }$$
The M/M/m queuing system
M/M/m 排队系统考虑有一个队列和m个服务器的情况。该排队系统的状态转移图如下:
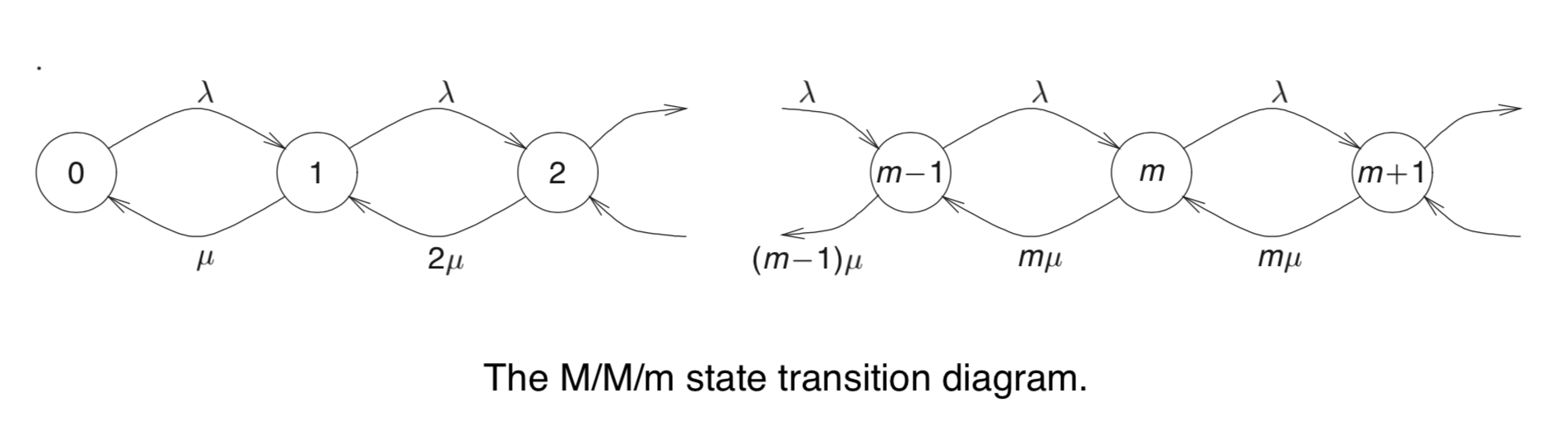
M/M/m 排队系统的性质:
- 因为只有一个队列,因此所有的状态下,到达速率都是常数
$\lambda$ - 如果系统内人数小于或等于m,那么队列一定为空。且状态k的服务速率为
$\mu_{k}=k \mu$,这是因为此时系统内的所有人都正在接受服务 - 如果系统内人数大于m,那么至少有一个人在队列中排队等待
各状态下的到达速率和服务速率分别为:
$$\begin{aligned} \lambda_{k} &=\lambda, \quad k=0,1,2, \ldots \\ \mu_{k} &=\left\{\begin{array}{ll}{k \mu} & {k=0,1,2, \ldots, m-1, m} \\ {m \mu} & {k \geq m}\end{array}\right.\end{aligned}$$
如果系统处于稳定状态,由状态k进入状态k-1的通量和状态k-1进入状态k的通量相等可知:
$$\begin{aligned} \lambda P_{k-1} &=k \mu P_{k}, \quad k \leq m \\ \lambda P_{k-1} &=m \mu P_{k}, \quad k \geq m \end{aligned}$$
首先考虑 k < m 的情况:
$$P_{k}=\frac{1}{k}(\rho m) P_{k-1}, \qquad \frac{\lambda}{\mu}=\rho m$$
递推可得:
$$\begin{aligned} P_{1} &=(\rho m) P_{0} \\ P_{2} &=\frac{(\rho m)}{2} P_{1}=\frac{(\rho m)^{2}}{2 !} P_{0} \\ P_{3} &=\frac{(\rho m)}{3} P_{2}=\frac{(\rho m)^{3}}{3 !} P_{0} \end{aligned}$$
故 k < m 时的一般式为:
$$P_{k}=\left(\frac{(m \rho)^{k}}{k !}\right) P_{0}, \qquad k<m$$
再考虑 k > m 的情况:
$$P_{k}=\frac{\lambda}{m \mu} P_{k-1}=\rho P_{k-1}$$
递推可得:
$$\begin{aligned} P_{m} &=\rho P_{m-1} \\ P_{m+1} &=\rho P_{m}=\rho^{2} P_{m-1} \\ P_{m+2} &=\rho P_{m+1}=\rho^{3} P_{m-1} \end{aligned}$$
故 k > m 时的一般式为:
$$P_{k}=\rho^{k-m+1} P_{m-1} \qquad k=m, m+1, \ldots$$
由 k < m 情况下的概率分布函数$P_{k}$,可知:
$$P_{m-1}=\left(\frac{(m \rho)^{m-1}}{(m-1) !}\right) P_{0}$$
由上述两式整理得:
$$P_{k}=\left(\frac{m^{m} \rho^{k}}{m !}\right) P_{0}, \quad k=m, m+1, \ldots$$
综上,稳定状态下,M/M/m 排队系统的状态概率分布为:
$$P_{k}=\left\{\begin{array}{l}{P_{0}\left(\frac{(m \rho)^{k}}{k !}\right) \qquad k \leq m} \\ {P_{0}\left(\frac{m^{m} \rho^{k}}{m !}\right) \quad k \geq m}\end{array}\right.$$
其中,$\rho=\frac{\lambda}{m \mu}<1$。
下面计算$P_{0}$,由于:
$$\sum_{k=0}^{\infty} P_{k}=1$$
可得:
$$P_{0}\left[\sum_{k=0}^{m-1} \frac{(m \rho)^{k}}{k !}+\sum_{k=m}^{\infty} \frac{m^{m} \rho^{k}}{m !}\right]=1$$
故当$\rho<1$时,M/M/m 排队系统的稳定状态概率分布为:
$$\boxed{ P_{k}=\left\{\begin{array}{ll}{P_{0}\left(\frac{(m \rho)^{k}}{k !}\right)} & {k \leq m} \\ {P_{0}\left(\frac{m^{m} \rho^{k}}{m !}\right)} & {k \geq m}\end{array}, \quad \rho=\frac{\lambda}{m \mu}<1\right. }$$
其中,$P_{0}=\left[\sum_{k=0}^{m-1} \frac{(m \rho)^{k}}{k !}+\frac{(m \rho)^{m}}{m !(1-\rho)}\right]^{-1}$。
Note: 对于M/M/m 排队系统,一个重要的问题是系统内需要排队的概率。当系统内人数大于服务器数量时,顾客需要排队。需要排队的概率为:
$$P_{k \geq m+1}=\sum_{k=m+1}^{\infty} P_{k}=\sum_{k=m}^{\infty} P_{k}-P_{m}=P_{0}\left(\frac{m^{m} \rho^{m+1}}{m !(1-\rho)}\right)$$
The M/M/1/m queuing system
在之前的模型中,我们总是假设队列的长度是无限的。但现实中,由于缓存的限制,队列的长度通常是有限的。
在一个M/M/1/m 排队系统中,如果系统内人数为m,那么任何后来者的服务请求都会被拒绝。对于M/M/1/m 排队系统,由于系统最多只能容纳m位顾客,且正在接受服务的那位顾客同样也需要占用1个位置,因此排队等待接受服务的队列的最大长度为m-1。
M/M/1/m 排队系统的状态转移图如下:
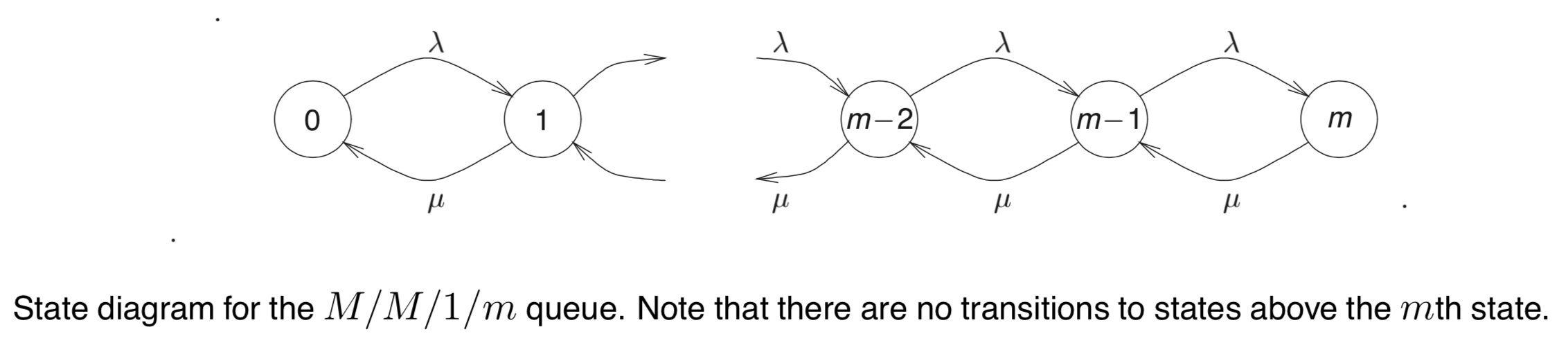
M/M/1/m 排队系统的前半部分推导过程和M/M/1 排队系统十分相像。唯一的区别在于,由于M/M/1/m 排队系统在状态k处截断,故其$P_0$值与M/M/1 排队系统的$P_0$值不同。
下面是M/M/1/m 排队系统的通量图:
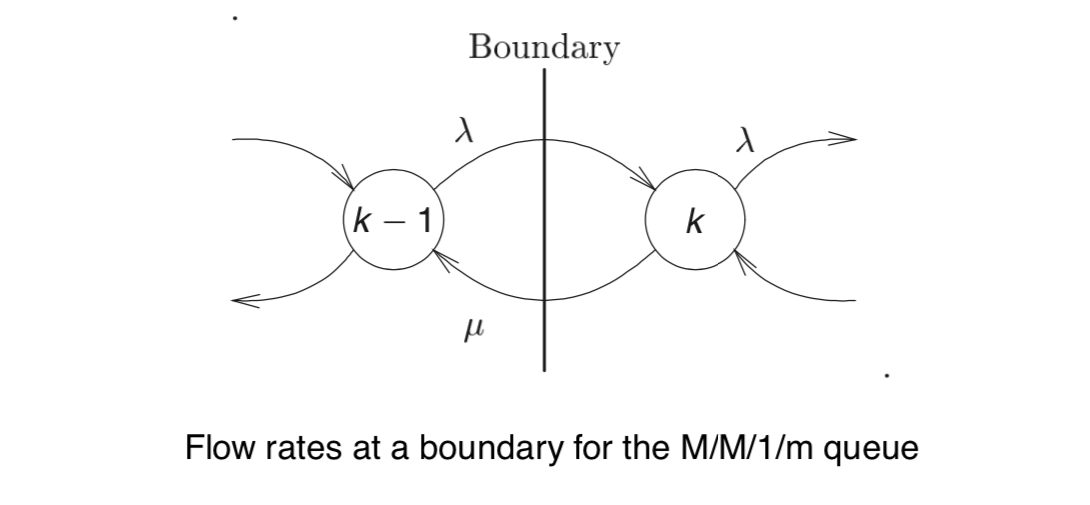
由通量图可知:
$$\lambda_{k-1} P_{k-1}+\mu_{k+1} P_{k+1}=\mu_{k} P_{k}+\lambda_{k} P_{k}, \quad k=1, \ldots, m-1$$
解得:
$$\lambda_{k} P_{k}=\mu_{k+1} P_{k+1}, \qquad k=0, \dots, m-1$$
递推可得:
$$\begin{aligned} P_{1} &=\left(\frac{\lambda_{0}}{\mu_{1}}\right) P_{0} \\ P_{2} &=\left(\frac{\lambda_{1}}{\mu_{2}}\right) P_{1}=\left(\frac{\lambda_{0} \lambda_{1}}{\mu_{1} \mu_{2}}\right) P_{0} \\ P_{3} &=\left(\frac{\lambda_{2}}{\mu_{3}}\right) P_{1}=\left(\frac{\lambda_{0} \lambda_{1} \lambda_{2}}{\mu_{1} \mu_{2} \mu_{3}}\right) P_{0} \end{aligned}$$
由上述递推公式可知一般式为:
$$P_{k}=\left(\frac{\prod_{i=0}^{k-1} \lambda_{i}}{\prod_{i=1}^{k} \mu_{i}}\right) P_{0}=\left(\frac{\lambda}{\mu}\right)^{k} P_{0}, \qquad k=0, \ldots, m$$
下面求$P_0$,由于:
$$\sum_{i=0}^{m} P_{i}=\left(1+\rho+\rho^{2}+\cdots+\rho^{m}\right) P_{0}=1, \qquad \rho=\frac{\lambda}{\mu}$$
导出:
$$P_{0}=\frac{1-\rho}{1-\rho^{m+1}}$$
故M/M/1/m 排队系统在稳定状态下的概率分布为:
$$\boxed{ P_{k}=\frac{(1-\rho) \rho^{k}}{1-\rho^{m+1}} \qquad k=0, \ldots, m }$$
其中,$\rho=\frac{\lambda}{\mu}$。
The M/M/∞ queuing system
M/M/∞ 排队系统考虑有一个队列,无穷个服务器的情况。下面是M/M/∞ 排队系统的状态转移图:
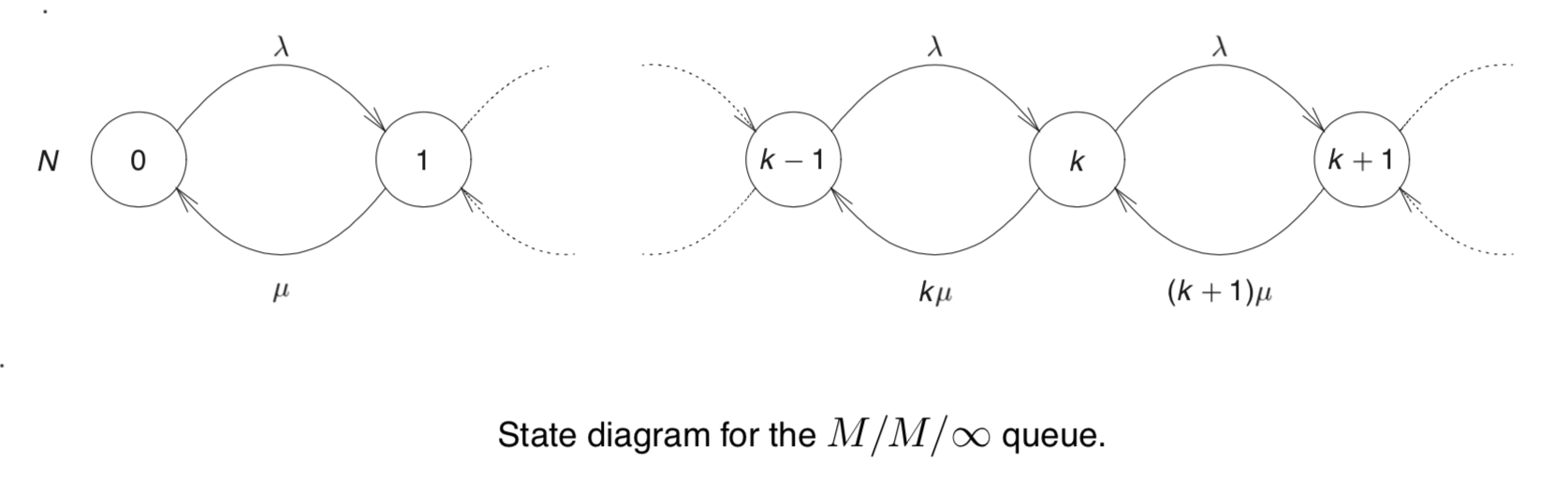
通量图如下:
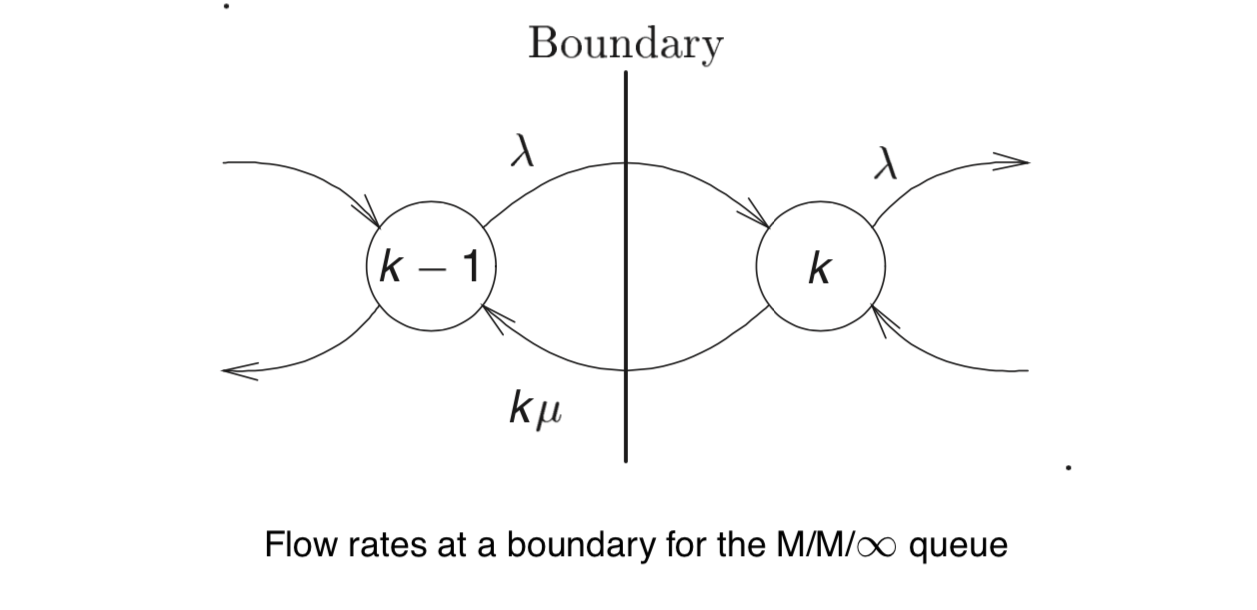
由通量图可知:
$$\lambda_{k-1} P_{k-1}=\mu_{k} P_{k}$$
又$\lambda_{k}=\lambda, \mu_{k}=k \mu$,等式可化为:
$$\lambda P_{k-1}=k \mu P_{k}$$
由递推公式可得:
$$P_{k}=\frac{1}{k !}\left(\frac{\lambda}{\mu}\right)^{k} P_{0}$$
依照之前的方法,求出$P_0$为:
$$P_{0}=\left[\sum_{k=0}^{\infty}\left(\frac{\lambda}{\mu}\right)^{k} \frac{1}{k !}\right]^{-1}=\exp \left(-\frac{\lambda}{\mu}\right)$$
综上,M/M/∞ 排队系统的状态概率分布为:
$$\boxed { P_{k}=\frac{1}{k !}\left(\frac{\lambda}{\mu}\right)^{k} \exp \left(-\frac{\lambda}{\mu}\right) }$$
The M/M/m/m queuing system
M/M/m/m 排队系统有m个服务器,同时系统内最多容纳m位顾客。它的状态转移图如下:
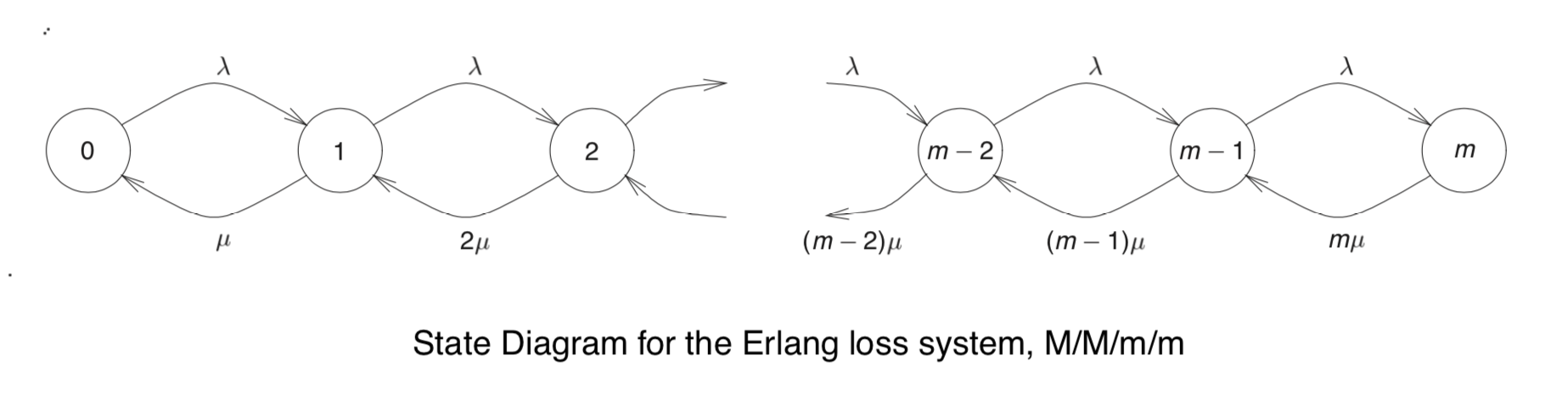
到达速率和服务速率表达如下:
$$\lambda_{k}=\left\{\begin{array}{cl}{\lambda} & {k=0,1, \ldots, m-1} \\ {0} & {k \geq m}\end{array}\right.$$
$$\mu_{k}=\left\{\begin{array}{ll}{k \mu} & {k=0,1, \ldots, m} \\ {0} & {k>m}\end{array}\right.$$
通量图如下:
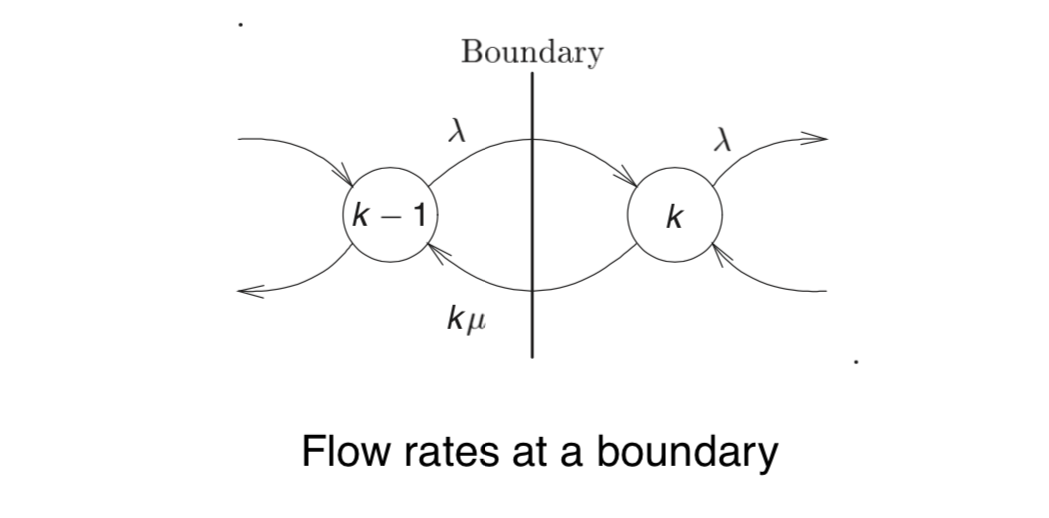
由通量图可得:
$$\lambda P_{k-1}=k \mu P_{k}, \qquad k=1, \ldots, m$$
整理得:
$$P_{k}=\frac{\lambda}{k \mu} P_{k-1}=\frac{a}{k} P_{k-1}, \qquad k=1, \ldots, m$$
由递推公式解得:
$$P_{k}=P_{0}\left(\prod_{n=1}^{k} \frac{a}{n}\right)=\frac{a^{k}}{k !} P_{0}, \quad k=0, \ldots, m$$
下面计算$P_0$,由于:
$$P_{0} \sum_{k=0}^{m} \frac{a^{k}}{k !}=1$$
故:
$$P_{0}=\frac{1}{\sum_{k=0}^{m} \frac{a^{k}}{k !}}$$
因此,M/M/m/m 排队系统的状态概率分布为:
$$\boxed { P_{k}=\frac{\frac{a^{k}}{k !}}{\sum_{n=0}^{m} \frac{a^{n}}{n !}}, \qquad a=\frac{\lambda}{\mu}, \qquad k=0, \ldots, m }$$