跟李沐老师学深度学习,课程见 d2l,如有错误,欢迎拍砖
GitHub 项目地址:AI-Project
〇、技术路线图
flowchart TD
A[softmax 回归] -->|无法拟合 XOR 函数| B[多层感知机]
B --> |高像素图片作为输入,模型参数爆炸| C[卷积]
C -->|数据的长宽下降太快| D[填充]
C -->|数据的长宽下降太慢| E[步幅]
C -->|缓解卷积对位置敏感| F[池化]
C -->|多模式识别与组合| G[多通道输入/输出]
一、softmax 回归
1. 虽然叫回归,但是softmax 解决的是分类问题
- 回归估计是一个连续值
- 分类预测是一个离散类别
2. 分类应用举例
- MINIST
- ImageNet
- human-protein-atlas-image-classification (Kaggle)
- malware-classification (Kaggle)
- jigsaw-comment-classification (Kaggle)
3. 从回归到多类分类 – 均方损失
对分类结果做 one-hot 编码:
$y = [y_1, y_2, , ... , y_n]^T$
$y_i=\left\{\begin{array}{l}1 \text { if } i=y \\ 0 \text { otherwise }\end{array}\right.$
使用均方损失 ($O_i$) 训练:
$\hat{y}=\underset{i}{\operatorname{argmax}} o_i$
该式含义为:取最大化 $O_i$ 对应的 $i$ 作为 $\hat{y}$ 的估计值
4. 无校验比例
需要更置信地识别正确类(大余量)
$O_y - O_i \geq \Delta (y, i)$
5. 校验比例
现在我们得到的输出 $O_i$ 是一个向量,我们希望把它转化成每一种分类对应的概率。我们可以通过添加 softmax 操作子实现这一目标,它对 $O_i$ 做如下操作:
$\hat{y_i} = \frac{\exp(O_i)}{\sum_{k} \exp(O_k)}$
此时,$y$ 与 $\hat{y}$ 都是概率,我们可以把两个概率的区别 $y - \hat{y}$ 作为损失
6. 交叉熵损失
交叉熵常用来衡量两个概率的区别 $H(p, q) = \sum_{i} - P_i log(q_i)$
将它作为损失:
$l(\mathbf{y}, \hat{\mathbf{y}})=-\sum_i y_i \log \hat{y}_i=-\log \hat{y}_y$
PS:因为除了 $i = y$ 的情况,$i$ 为其他值时 $y_i$ 为 0
其梯度是真实概率和预测概率的区别:
$\partial_{o_i} l(\mathbf{y}, \hat{\mathbf{y}})=\operatorname{softmax}(\mathbf{o})_i-y_i$
7. 总结
- Softmax回归是一个多类分类模型
- 使用Softmax操作子得到每个类的预测置信度
- 使用交叉熵来衡量预测和标号的区别
二、多层感知机
感知机解决的是二分类问题
1. 什么是感知机
给定输入 $x$,权重 $w$,和偏移 $b$,感知机输出:
$o = \sigma \left(\left<W, X\right> + b\right)$
$\sigma(x) = \left\{\begin{array}{l}1 \text { if } x > 0 \\ -1 \text { otherwise }\end{array}\right.$
2. 训练感知机
- 初始化:w = 0, b = 0
- 如果分类分错:
$y_i [\left< W, X_i \right>] \leq 0 \text{ then } w \gets w + y_i x_i \text{ and } b \gets b + y_i $ - 停止条件:所有类别都分对的时候停止
等价于使用批量大小为1的梯度下降,并使用如下损失函数:
$l\left(y, X, W\right) = max\left(0, -y\left<W, X\right>\right)$
3. 收敛定理
对于:
- 数据在半径
$r$内 - 余量
$\rho$将数据点分两类 $\lvert\lvert w \rvert\rvert^{2} + b^2 \leq 1$
感知机保证在 $\frac{r^2 + 1}{\rho^2}$ 步后收敛
4. XOR问题 (Minsky & Papert, 1969)
感知机不能拟合 XOR 函数,它只能产生线性分割面
|
1 | -1
|
-----------------
|
-1 | 1
|
由于感知机无法拟合 XOR 函数,导致了第一次 AI 寒冬。但是其实有办法解决这个问题,解决的方法叫 多层感知机。
5. 多层感知机
|
① | ②
|
-------------------
|
③ | ④
|
- 先学一次:对于竖线,左边为
$+$,右边为$-$ - 再学一次:对于横线:上边为
$+$,下边为$-$
把两次分类结果组合一下(做乘法),就能表达 XOR 了。
对于我们的启发是:如果一个复杂问题一次性做不了,可以先用一个简单函数,再用一个简单函数,接着用一个简单函数组合这两者。也就是一层变多层,就可以表达复杂结果。

为什么说隐藏层的层数是超参?因为输入数据的维度 $n$ 和输出数据的维度 $m$ 都是由数据决定的,我们惟一能调的,只有隐藏层的层数。
6. 单隐藏层
- 输入:
$\mathbf{x} \in \mathbb{R}^{n}$ - 隐藏层:
$\mathbf{W}_1 \in \mathbb{R}^{m \times n}, \mathbf{b}_1 \in \mathbb{R}^m$ - 输出层:
$\mathbf{w}_2 \in \mathbb{R}^{m}, \mathbf{b}_2 \in \mathbb{R}$
$~~~~~~~~~\mathbf{h} = \sigma \left( \mathbf{W}_1 + \mathbf{b}_1 \right)$
$~~~~~~~~~\mathbf{o} = \mathbf{w}_2^\mathbf{T} \mathbf{h} + \mathbf{b}_2$
$\sigma$ 是按元素的激活函数
Note: 为什么需要非线性的激活函数?
如果
$\sigma$是线性的,把公式一的$\mathbf{h}$代入到公式二中,可得:
$\mathbf{hence} \space \mathbf{o} = \mathbf{w}_2^T \mathbf{W}_1 \mathbf{o} + b^{\prime}$依然是线性,折腾半天发现我们得到的依旧是一个最简单的线性模型。
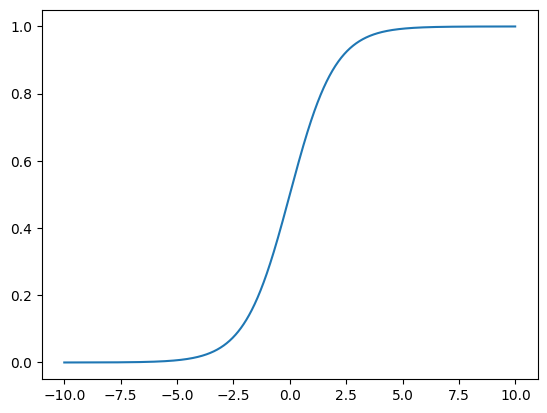
7. Sigmoid 激活函数
将输入投影到 $(0, 1)$
$sigmoid(x) = \frac{1}{1 + \mathbf{exp}(-x)}$
8. Tanh 激活函数
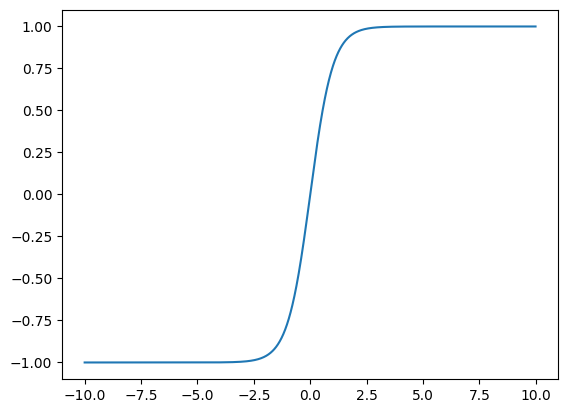
将输入投影到 $(-1, 1)$
$tanh(x) = \frac{1 - \mathbf{exp}(-2x)}{1 + \mathbf{exp}(-2x)}$
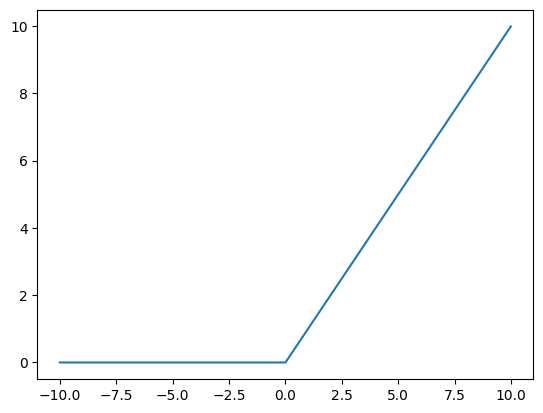
9. ReLU 激活函数
ReLU: rectified linear unit
将输入投影到 $(0, +\infty)$
$ReLU(x) = \mathbf{max}(x, 0)$
指数运算是一个很贵的操作,所以为什么大家爱用ReLU,因为一个max就好了
10. 多类分类:借鉴 softmax
$softmax$ 就是输出一个堆概率 $y_1, y_2, ..., y_k$,所有这些加起来等于1
$y_1, y_2, ..., y_k = softmax(o_1, o_1, ... , o_k)$
11. 多隐藏层
$\mathbf{h}_1 = \sigma(\mathbf{W}_1\mathbf{x} + b_1)$
$\mathbf{h}_2 = \sigma(\mathbf{W}_2\mathbf{h}_1 + b_2)$
$\mathbf{h}_3 = \sigma(\mathbf{W}_3\mathbf{h}_2 + b_3)$
$\mathbf{o} = \mathbf{W}_4\mathbf{h}_3 + b_4$
激活函数主要是为了防止层数的塌陷,所以最后一层输出层不需要激活函数。
超参数:
- 隐藏层数
- 每层隐藏层的大小
12. 总结
- 多层感知机使用隐藏层和激活函数来得到非线性模型
- 常用激活函数是Sigmoid, Tanh, ReLU
- 使用Softmax来处理多类分类
- 超参数为隐藏层数,和各个隐藏层大小
三、卷积层
一张 12,000,000 像素的猫或者狗的图片,分RGB三种颜色,如果使用单隐藏层的 MLP 处理,模型有 3.6B 个参数,远多于世界上所有猫和狗的数量。
1. 识别器的原则
- 平移不变性(在图片的哪个位置都能识别到)
- 局部性(不需要看整张图就能识别)
2. 重新考察全连接层
- 将输入和输出变形为矩阵(宽度,高度)
- 将权重变形为4-D张量
$(h, w)$到$(h^\prime, w^\prime)$$h_{i,j} = \sum_{k,l} w_{i,j,k,l}x_{k,l} = \sum_{a,b} v_{i,j,a,b}x_{i+a,j+b}$ $v$是$w$的重新索引$v_{i,j,i+a,j+b}$
3. 原则 #1 - 平移不变性
- x的平移导致h的平移
$h_{i,j} = \sum_{a,b} v_{i,j,a,b} x_{i+a,j+b}$ - v不应该依赖于(i, j)
- 解决方案:
$v_{i,j,a,b} = v_{a,b}$$h_{i,j} = \sum_{a,b} v_{a,b}x_{i+a,j+b}$
这就是二维卷积交叉相关
4. 原则 #2 - 局部性
$h_{i,j} = \sum_{a,b} \mathbf{v}{a,b} \mathbf{x}{i+a,j+b}$
- 当评估
$h_{i,j}$时,我们不应该用远离$x_{i,j}$的参数 - 解决方案:当
$|a|, |b| > \Delta$ 时,使得 $v_{a,b} = 0$$h_{i,j} = \sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta} v_{a,b} x_{i+a,j+b}$
5. 小结
- 对全连接层使用平移不变性和局部性得到卷积层
$~~~~~~~~~~~h_{i,j} = \sum_{a,b} \mathbf{v}_{i,j,a,b} \mathbf{x}_{i+a,j+b}$
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$⬇
$~~~~~~~~~~~h_{i,j} = \sum_{a=-\Delta}^{\Delta} \sum_{b=-\Delta}^{\Delta} \mathbf{v}_{a,b} \mathbf{x}_{i+a,j+b}$
6. 二维交叉相关
- 卷积核 (Kernel),其实就是
$\mathbf{w}$ - 核是不随扫描的位置变化的,这就实现了平移不变性
7. 二维卷积层
- 输入
$\mathbf{X}: n_h \times n_w$ - 核
$\mathbf{W}: k_h \times k_w$ - 偏差
$b \in \mathbb{R}$ - 输出
$\mathbf{Y}: (n_h - k_h + 1) \times (n_w - k_w + 1)$
$\mathbf{Y} = \mathbf{X} \mathbf{W} + b$
$\mathbf{W}$ 和 $b$ 是可学习的参数
8. 例子
不同的卷积核,会得到不同的效果
边缘检测
$\left[\begin{array}{c} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{array}\right]$

锐化
$\left[\begin{array}{c} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \end{array}\right]$

高斯模糊
$\frac{1}{16}\left[\begin{array}{c} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array}\right]$

9. 交叉相关 vs 卷积
- 二维交叉相关
- 二维卷积
- 由于对称性,在实际使用中没有区别
因为使用是一样的,所以没有使用数学上严格定义的卷积
10. 一维和三维交叉相关
- 一维:文本、语言、时需序列
- 二维:视频、医学图像、气象图像
11. 总结
- 卷积层将输入和核矩阵进行交叉相关,加上偏移后得到输出
- 核矩阵和偏移是可学习的参数
- 核矩阵的大小是超参数
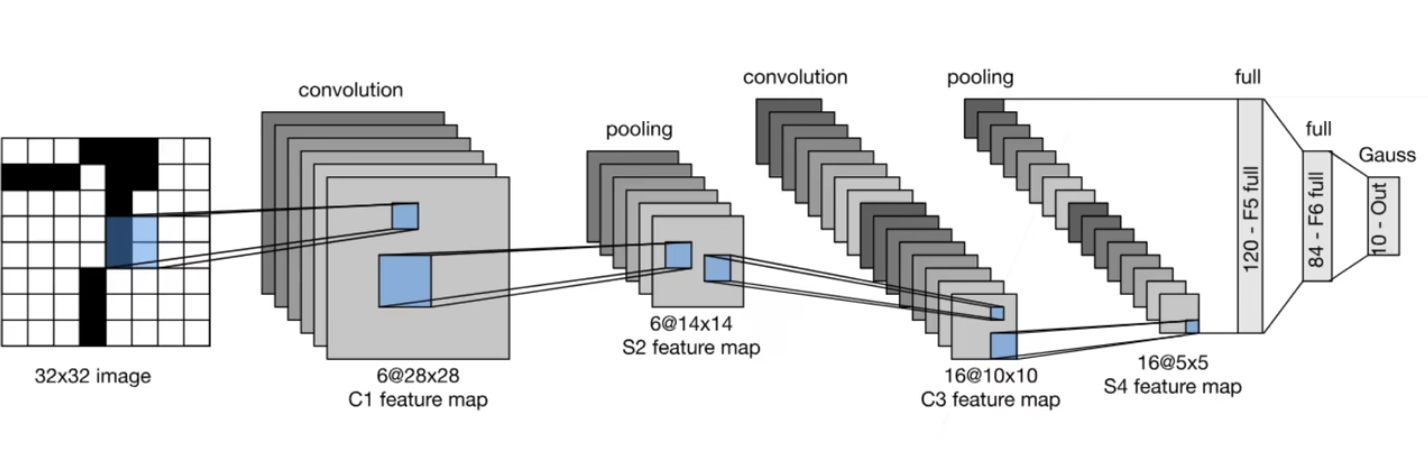
四、LeNet
LeNet is a convolutional neural network structure proposed by LeCun et al. in 1998.
最早应用于手写数字识别。
MNIST 是 LeNet 附带的数据集
- 5w个训练数据
- 1w个测试数据
- 图像大小$28 \times 28$
- 10类
1. 小结
- LeNet是早期成功的神经网络
- 先使用卷积层来学习图片空间信息
- 然后使用全连接层来转换到类别空间
2. 卷积神经网络(LeNet)
LeNet (LeNet-5) 由两个部分组成:卷积编码器和全连接层密集块
五、AlexNet
1. 技术回顾
1)支持向量机
在2000年左右,最流行的机器学习的算法是核方法 (Learning with Kernels).
the Support Vector Machine (SVM)
- 特征提取
- 选择核函数来计算相似性
- 凸优化问题
- 漂亮的定理(来自泛函)
优点:对调参不敏感,闭着眼睛都可以用
2)几何学
- 抽取特征
- 描述几何(例如多相机)
- (非)凸优化
- 漂亮定理
- 如果假设满足,效果很好
3)特征工程
直接把特征放到SVM里效果非常差,所以需要做特征工程
- (在计算机视觉里)特征工程是关键
- 特征描述子:SIFT, SURF
2. ImageNet (2020)
- 图片:自然物体的彩色图片
- 大小:$469 \times 387$
- 样本数 1.2M
- 类数:1000
因为你有了更大的数据集,所以允许用更深的神经网络,用来抽取信息
3. AlexNet
- AlexNet赢了2012年ImageNet竞赛
- 更深更大的 LeNet
- 主要改进:
- 丢弃法(因为模型大了,所以用丢弃做一点正则)
- ReLU($Sigmoid \space (LeNet) \to ReLU$,ReLU在零点的一阶导更好,梯度更大)
- MaxPooling(数值比较大,梯度比较大,使得训练比较容易)
- 计算机视觉方法论的改变
- 核方法:人工特征提取 $\to$ SVM
- 神经网络:通过 CNN 学习特征 $\to$ Softmax回归
4. AlexNet架构
1)第一个卷积层和池化层的区别
| AlexNet | LeNet |
|---|---|
| image ($3 \times 224 \times 224$) | image ($32 \times 32$) |
| 11*11 Conv(96), stride 4 | 5*5 Conv(6), pad 2 |
| 3*3 MaxPool, stride 2 | 2*2 AvgPool, stride 2 |
- 卷积:更大的窗口,更大的通道数,更大的步幅
- 池化:更大的窗口且stride不变(对位置更不敏感),使用MaxPool
2)接下来
| AlexNet | LeNet |
|---|---|
| 5*5 Conv(256), pad 2 | 5*5 Conv() |
| 3*3 MaxPool, stride 2 | 2*2 AvgPool, stride 2 |
| 3*3 Conv(384), pad 1 | |
| 3*3 Conv(384), pad 1 | |
| 3*3 Conv(384), pad 1 | |
| 3*3 MaxPool, stride 2 |
- 新增了3层卷积层
- 更多的输出通道
3)全连接层
| AlexNet | LeNet |
|---|---|
| Dense(4096) | Dense(120) |
| Dense(4096) | Dense(84) |
| Dense(1000) | Dense(10) |
- 隐藏层大小:120 $\to$ 4096
- 输出类别:10 $\to$ 1000
5. 更多细节
- 激活函数从 Sigmoid 变到了 ReLU(减缓梯度消失,因为梯度比较大)
- 隐藏全连接层后加入了丢弃层
- 数据增强(随机截取采样,调亮度/色温。神经网络会记住所有数据,数据增强能让记住数据的能力变低)
6. 总结
- AlexNet是更大更深的LeNet,10x参数个数,260x计算复杂度
- 新加入了丢弃法,ReLU,最大池化层,和数据增强
- AlexNet赢下了2012ImageNet竞赛后,标志着新的一轮神经网络热潮的开始

